- (a)
- Find the Taylor series about x=0 of
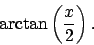
- (b)
- What is the radius of convergence of this series?
- (a)
- Find an equation for the tangent plane to the graph of
f(x,y) = xy + y2 + e2x at (0,2,5).
- (b)
- Find an equation for plane parallel to
this tangent plane
containing the point (1,1,0).
- (c)
- Where does the line perpendicular to this new plane and containing (1,1,0) hit the original tangent plane.
Note: If you have already tried this the point was meant to be
not
as stated. Both ways are doable but this second point is much easier.
- (a)
- Express f as a composite of a function
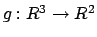 and
a function
and
a function
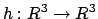 .
.
- (b)
- Find Dh and Dg (Df refers to the derivative of f).
- (c)
- Use the chain rule to compute
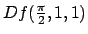 .
.
- (d)
- Find the kernel of
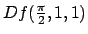 .
.
![\begin{displaymath}M_{\lambda} = \left[\begin{array}{rr} \lambda & 0 \\ 0 & 1 \end{array}
\right]
\end{displaymath}](img10.gif)
is a stretch of the plane by
- (a)
- Express A as a matrix.
- (b)
- In each of the following cases describe the rank of A, and find a
non-zero polynomial in A's kernel whenever such an element exists.
- i.
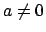 and
and 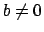 and
and 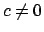 .
.
- ii.
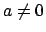 and
and 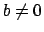 and c = 0.
and c = 0.
- iii.
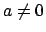 and b = 0 and c = 0.
and b = 0 and c = 0.
- (a)
- Find the general solution to
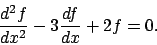
- (b)
- Use the previous problem (problem 7(a)) to find a polynomial solution to
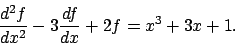
- (c)
- Find a solution to
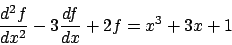
satisfying f(0)=1 and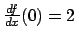 .
Note: you are the right track if you get coeffeicients wich are rational
numbers with denominators like 8.
.
Note: you are the right track if you get coeffeicients wich are rational
numbers with denominators like 8.