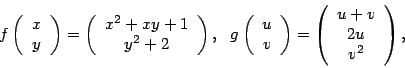
COVERED TODAY: The Chain Rule. The method used in class is not in the book.

DUE NEXT TIME:

(1) Given that

$$f\left( \begin{array}{c} x y \end{array} \right)=\left( \b... ...)=\left( \begin{array}{c} u+v 2u v^2 \end{array} \right),$$

find the derivative matrix of the composite function $g \circ f$ at $(x,y)=(1,1)$. Do the same at $(x,y) = (0,0)$.

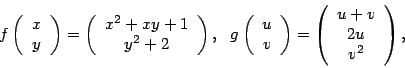
(2) Consider the function $f:R \longrightarrow R^3$ given by:

$$f(t) = \left( \begin{array}{c} t t^2-4 e^{t-2} \end{array}\right).$$

Let $g:R^3 \longrightarrow R$ be a differentiable function. If $x_\circ = (2,0,1)$, and

$$\frac{\partial g}{\partial x}(x_\circ) = 4, \frac{\partia... ...(x_\circ) = 2, \frac{\partial g}{\partial z}(x_\circ) = 2,$$

find $d(g \circ f) /dt$ at $t=2$.

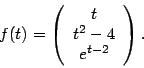
(3) The functions $f$ and $g$ are defined by

$$f\left( \begin{array}{c} u v \end{array} \right) = \left( \... ...}{l} 0 < u < \infty, -\pi/2 < v < \pi/2, \end{array} \right.$$

$$g\left( \begin{array}{c} x y \end{array} \right) = \left( \... ...displaystyle \frac{y}{x}}\end{array}\right), 0 < x< \infty.$$

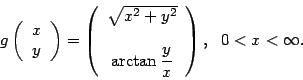
(a) Find the derivative matrix of $g \circ f$ at $\left( \begin{array}{c}u v \end{array} \right)$.

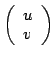(b) Find the derivative matrix of $f \circ g$ at $\left( \begin{array}{c}x y \end{array} \right)$.

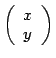>From the Textbook, Section 15.5:

3

4

10

14

22

28

33

43