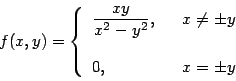COVERED TODAY: The derivative matrix and differentiability. (This is not in the book.)
DUE NEXT TIME:
For each of the following functions ![]() find the derivative matrix
find the derivative matrix
![]() :
:
(1)
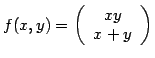
(2)
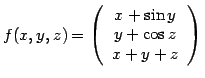
(3)
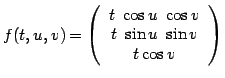
(4)
![]()
For the following functions find the derivative matrix at the indicated
point:
(5)
![]() at
at ![]()
(6)
![]() at
at
![]()
(7) Let
![]() be a linear transformation with
matrix
be a linear transformation with
matrix
![]() , i.e.
, i.e. ![]() . What is the dervative matrix of
. What is the dervative matrix of ![]() ?
?
(8) A translation is a function of the form ![]() , for a
fixed vector
, for a
fixed vector ![]() . What is the derivative matrix of a translation from
. What is the derivative matrix of a translation from
![]() to
to ![]() ?
?
(9) Consider the function
![]() defined by
defined by
![]() . Prove that
. Prove that
![]() , for any
, for any ![]() and
and ![]() in
in ![]() .
.
(10) Verify that the function