DISCLAIMER: While I would consider this an appropriate final exam, it should in no way
be interpreted as a comprehensive list of topics to study for the actual final exam. We covered
far too many topics in this course for them all to appear on any single 2-hour exam.
Thus there are likely to be topics covered on the final which do not appear here and there are
likely to be topics covered here which will not appear on the final. I could go on disclaiming
for pages, but I hope you get the idea.
NOTE: Time-permitting, I will post solutions and/or hints. Keep your eye on the main math
23 web page. Also, I typed this up rather hastily, so there may be typos. Please let me know if
you find any.
NOTE #2: I'm not sure about this, but it is possible that this practice final might be a
bit long.
- 1.
- (a)
- Compute the Taylor series for
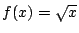 about x=1.
about x=1.
- (b)
- What is the interval of convergence of the series you found above? Justify your
answer.
- 2.
- Consider the linear homogeneous DE
y'' + p(t)y' + q(t)y = 0.
(assume p and q are continuous everywhere). Suppose that y1 and y2 are solutions to
the above DE. Prove that for any real numbers c1 and c2,
y=c1y1 + c2y2 is also a
solution to the same DE. Note that this is a theorem we proved in class. You are
therefore not allowed to merely quote it.
- 3.
- Solve the system of equations:
HINT:
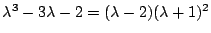 .
.
- 4.
- Find the general solution of the DE:
- 5.
- Consider the function f defined by
Find a Fourier sine series for f.
- 6.
- Suppose you have an elastic string of length 2 cm, and suppose that the ends of that string
are held fixed in such a way that a=1 (in the general wave equation
a2uxx=utt). Now
suppose you configure that string into the shape of the graph of the function f from the
previous problem, and then you release it (i.e. no initial velocity). Find a function u(x,t)
which describes the displacement of the string at location x at time t.
- 7.
- Suppose a mass of m kg is attached to a spring with spring constant k. Assume there is
no air resistance and assume there is no external force acting on the mass. Assume that the
mass is resting in its equilibrium position and, at time
t=0, it is flicked upward with an initial velocity of v0 m/s. Find a
function u(t) which
describes the position of the mass at any time t>0.
- 8.
- Solve the initial value problem:
- 9.
- Consider the linear homogeneous DE
Suppose that y1 and y2 are two solutions the above DE. Compute the Wronskian of y1 and
y2 (note that you need not know what y1 and y2 are in order to know their Wronskian).
- 10.
- Find the general solution of the DE:
Math 23 Fall 1999
1999-12-02
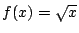 about x=1.
about x=1.
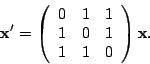
![]() .
.